Gravitational Field

Learning Outcomes

1. Show an understanding of the concept of a gravitational field as an example of field of force and define gravitational field strength as force per unit mass.
2. Recall and use Newton’s law of gravitation in the form $F=\frac{G{M}_1{M}_2}{r^2}$ .
3. Derive, from Newton’s law of gravitation and the definition of gravitational field strength, the equation  $g=\frac{\text{GM}}{r^2}$ for the gravitational field strength of a point mass.
4.  Recall and apply the equation $g=\frac{\text{GM}}{r^2}$   for the gravitational field strength of a point mass to new situations or to solve related problems.
5. Show an appreciation that on the surface of the Earth g is approximately constant and equal to the acceleration of free fall.
6. Define potential at a point as the work done in bringing unit mass from infinity to the point.
7. Solve problems using the equation  $\text{φ}=-\frac{\text{GM}}{r}$ for the potential in the field of a point mass.
8. Recognise the analogy between certain qualitative and quantitative aspects of gravitational and electric fields  (to be done together with the topic electric fields)
9. Analyse circular orbits in inverse square law fields by relating the gravitational force to the centripetal acceleration it causes.
10. Show an understanding of geostationary orbits and their application.

Introduction

In the topics of Dynamics, Forces, etc, we have been dealing with weights of different objects. Weight is a name given to the force acting on the object by gravity. In other words, weight is a gravitational force.

Gravitational force is a force that is evident in our everyday lives and plays a crucial role in many processes on Earth. For instance, the ocean tides are caused by the gravitational attraction of both the Moon and Sun on the earth’s oceans.

On Day 0, approximately twice a month, around new moon when the Sun, Moon, and Earth form a line (a condition known as syzygy), the tidal force due to the sun reinforces that due to the Moon.

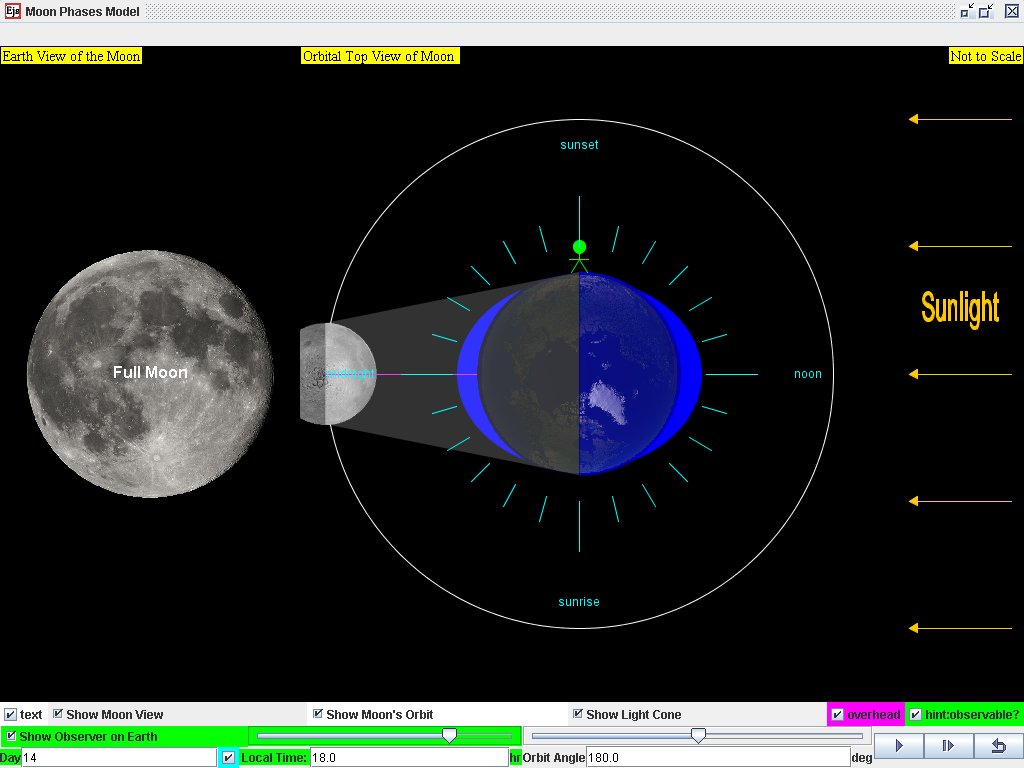
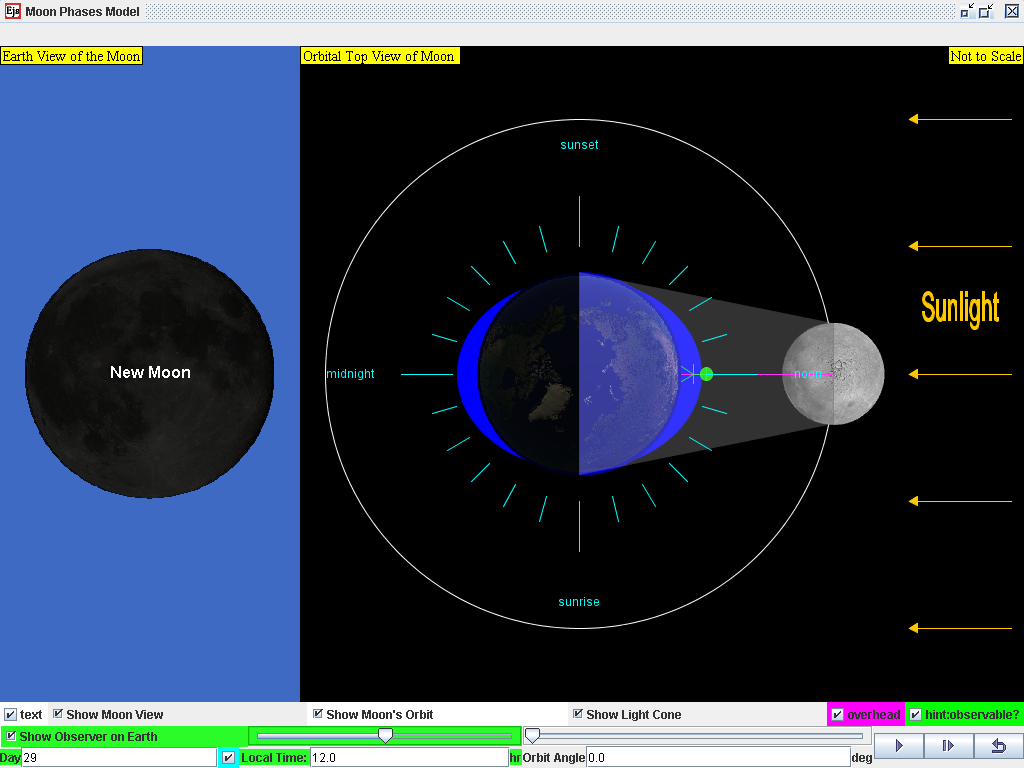
The java required model download here https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_MoonPhases.jar

At the end of the lunar cycle on the Day 29, 12 hours, around new moon when the Sun, Moon, and Earth form a line (a condition known as syzygy), the tidal force due to the sun reinforces that due to the Moon.

The falling of objects when released is also caused by the gravitational pull of the Earth on all objects. In terms of planetary motion, gravitational force is responsible for keeping the Earth in its orbit around the Sun, which in turns gives rise to four seasons in some countries.

Newton’s Law of Gravitation

Gravitation is a natural phenomenon by which physical bodies attract each other due to their masses. This force occurs whenever masses are present and the two bodies need not to be in contact with each other. It is however the weakest of the fundamental forces of nature.

In 1687, Sir Isaac Newton concluded that this non-contact gravitational force must be as responsible for the falling of the apple from a tree as it is the cause for the rotation of the moon about the earth. Hence he published the Newton’s law of gravitation which states that:

“The mutual force of attraction between any two point masses is
directly proportional to the product of their masses and
inversely proportional to the square of the separation between their centres.”

This means that if there are two point masses M and m and they are separated by distance r, the magnitude of the gravitational force attracting them to each other is

$|F|=\frac{G{M}_1{M}_2}{r^2}$

where G, the constant of universal gravitation, is $6.\text{67x1}{0}^{-11}\frac{N{m}^2}{k{g}^2}$ (will be given in data & formulae list during tests and examinations).

Note:
1.    r is taken to be the centre to centre distance (i.e. centre of particle to centre of particle). Do not take r to be the radius of orbit!
2.    This formula is an example of the inverse square law.

Inquiry:

1) What can you conclude about the two forces in the above diagram?

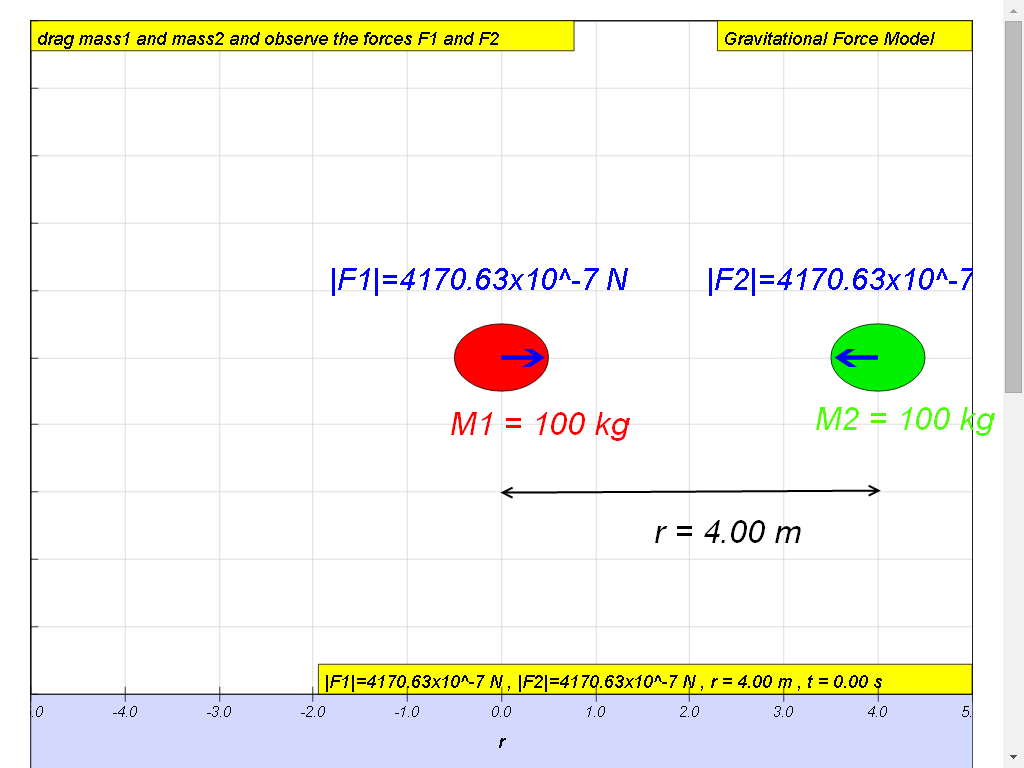
in the beginning, when t = 0.00 s, if M₁ = M₂ = 100 kg, r = 4.00 m, the forces F₁ (acts on M₁ points towards right or M₂)  and F2 (acts on M₂ points towards left or M₁) respectively can be calculate to be $|F|=\frac{G{M}_1{M}_2}{r^2}$ = $\frac{(6.\text{67x1}{0}^{-11})\left(100\right)\left(100\right)}{4^2}$= 4.17 x 10 ^-4 N

at time of collision, t = 0.24 s, r = 0.50 m, the forces F₁ (still acts on M₁ points towards right or M₂)  and F2 (acts on M₂ points towards left or M₁) respectively can be calculate to be $|F|=\frac{G{M}_1{M}_2}{r^2}$ = $\frac{(6.\text{67x1}{0}^{-11})\left(100\right)\left(100\right)}{{\mathrm{(0.5)}}^2}$ = 2.67 x 10 ^-2 N.

In the model below, you can drag to change the position of M₁ and M₂ to observe the directions of the F₁ and F₂ pairs. What can you conclude about the relationship about them?

Are they Newton's third law: action-reaction pair ( equal in magnitude, opposite in direction and act on different bodies).

Next, vary the mass of M₂ to zero value, what did you observe in terms of the magnitude/value of F₁ ? Can you conclude that F₁ and F₂ exists as a consequent of their masses influencing each other?

Hence, evidences suggests that the two forces in the diagram are action-reaction pair because each force is acting on the particle by the other particle.

2) In that case, when Earth pulls you down, why did you not pull Earth up?

To test this claim/question, let conduct an experiment. Set the initial values of if M₁ = 100 kg and M₂ = 1.00 kg, r = 4.00 m. Observe that forces are action-reaction pairs as predicted by Newton's Third Law. What will happen when the model is  'played'? Will M₁ and M₂ meet to the position x= 2.00 the middle? Will M₂ influence M₁?

Observe that the M₁ is indeed influenced by the M₂ because F₁ exists and M₁ did move a bit to the right. But because the mass M₁ is larger than , M₁ acceleration to the left is smaller.

Try for yourself, and key in the mass of Earth = 6.0x10²⁴ kg as 6e24 into the field for M₁ and your mass into the M₂ field.

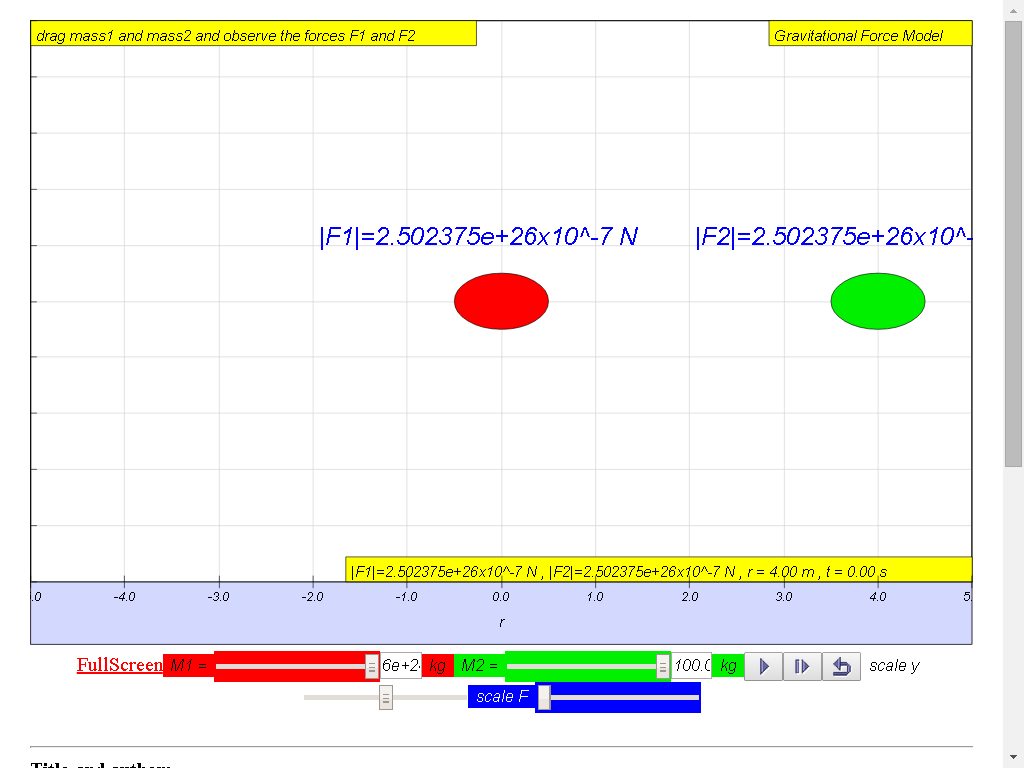
Click the play icon and what did you observe?

You did! it can be observe that the your mass M₂ did pull on Earth but the Earth only accelerate very little towards M₂.

Estimate the gravitational force exerted between you and your nearest neighbour in this lecture theatre.

answer:

Assume that both masses are 100 kg each and the distance between the centres of gravity of the two persons is 1.00 m.
Magnitude of the force $|F|=\frac{G{M}_1{M}_2}{r^2}$ = $\frac{(6.\text{67x1}{0}^{-11})\left(100\right)\left(100\right)}{1^2}$ =   = 6.67 x 10^-7 N
(Note:  This force is really small)

3) using the model, design an inquiry approach for asking the question:  is the relationship of the force on mass 1 due to mass 2, |F₁| and mass 2 due to mass 1 |F₂| on each other and their centre to centre distances apart r ?

(hints: ask the question:  is the relationship of the force on mass 1 due to mass 2, |F₁| and mass 2 due to mass 1 |F₂| on each other and their centre to centre distances apart r ? is the model$|F|=\frac{G{M}_1{M}_2}{r^2}$ valid?, plan what are the variables needed to test this model? collect the appropriate data, analyze the data,  explain the data, argue with the evidences your understanding, communicate the result)

Model:

https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_gravity01/gravity01_Simulation.xhtml