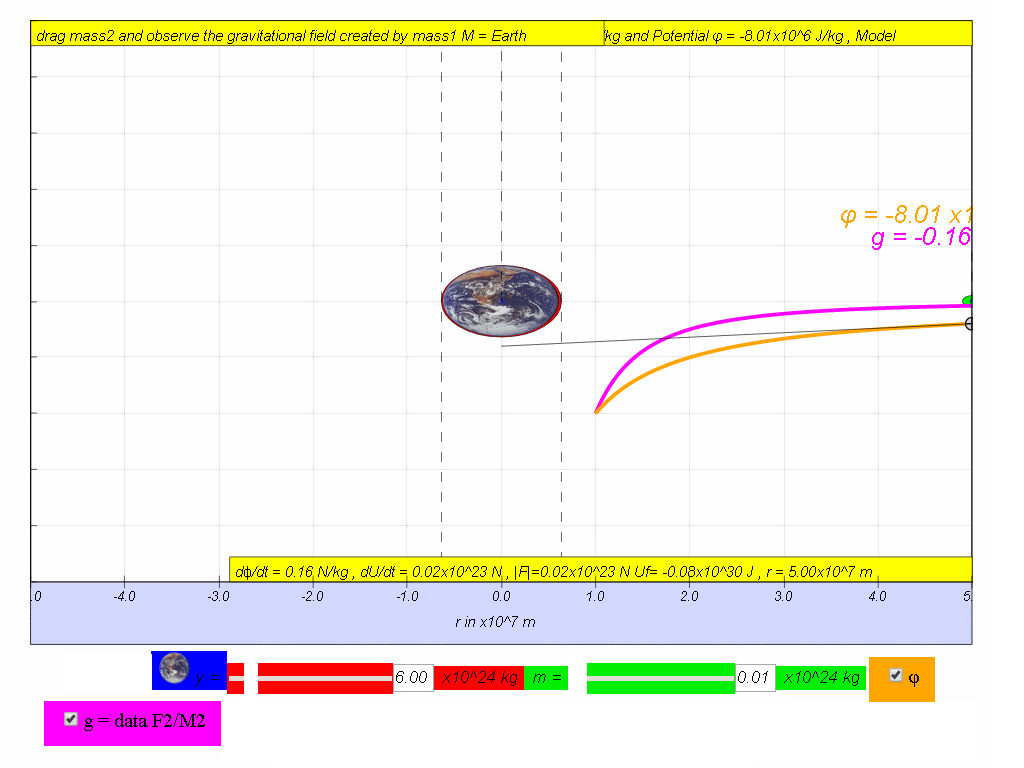
Values for the gravitational potential due to the Earth are given in the table below.
| Distance from Earth’s surface / m | Distance from Earth’s centre / m | Gravitational potential / MJ kg-1 | Gravitational Field Strength g / ms-2 | rate of change of potential with distance / ms-2 |
| 0 | 6 370 000 = 0.637x107 | -62.72 | ||
| 10 000 000 = 1x107 | -40.10 | |||
| 1.363x107 |
2.0x107 | -20.00 | ||
| 3.0x107 | -13.34 | -0.44 |
0.44 |
|
| 4.0x107 | -10.01 | |||
| 5.0x107 | -8.01 | -0.16 | 0.16 | |
| Infinity | 0 |
(i) given that radius of Earth = 6370 km, fill in the missing rows in the table for Distance from Earth’s surface / m.
(ii) Calculate the change in potential if an object travels from r = 5.0x107 m to r = 2.0x107 m

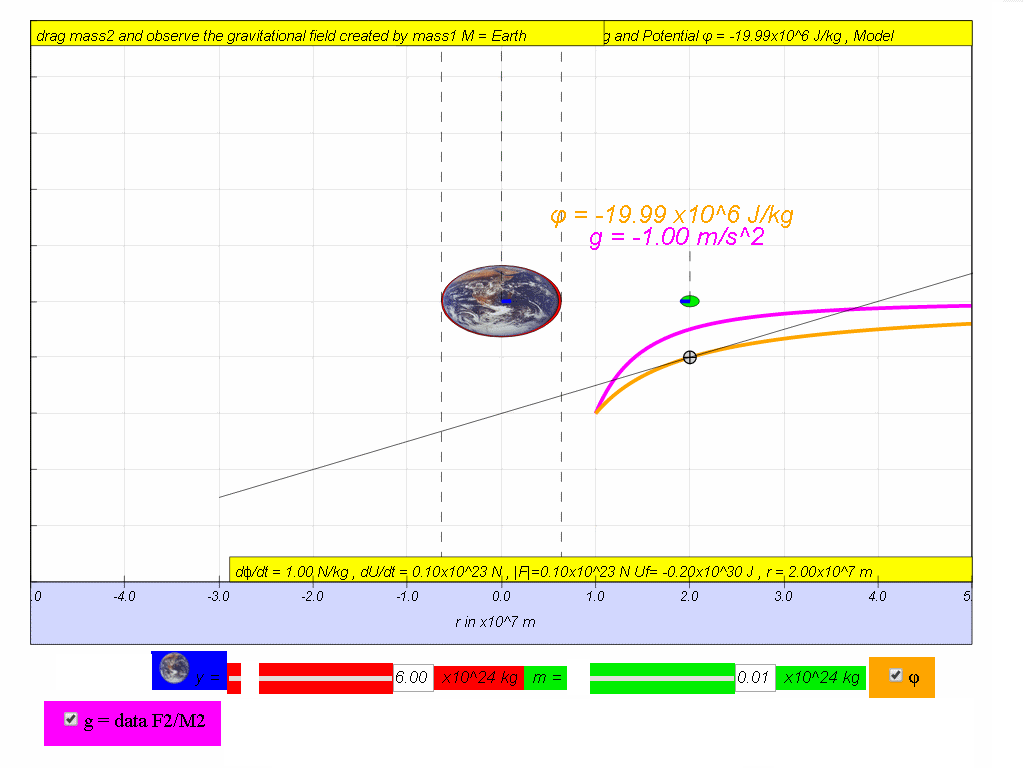
Answer: Δφ = φfinal - φinitial = -19.99x106 - (-8.01x106) = -11.95x106 J/kg
(ii) Hence or otherwise, calculate the change in potential energy if the object-satellite has a mass 0.01x1024 kg.
Answer: ΔPE = ΔU = m(Δφ) = 0.01x1024(-11.95x106) = -1.196x1029 J = -0.20x1030 J
(iii) Determine the potential energy lost by object-satellite of 0.07x1024 kg from a height of 13 630 000 to the Earth's surface.
Answer: ΔPE = m(Δφ) = 0.07x1024 (-6.67x10-11)(6.0x1024)() = (0.07x1024 )(-4.28x107 ) = 2.996x1030 = 3.00x1030 J
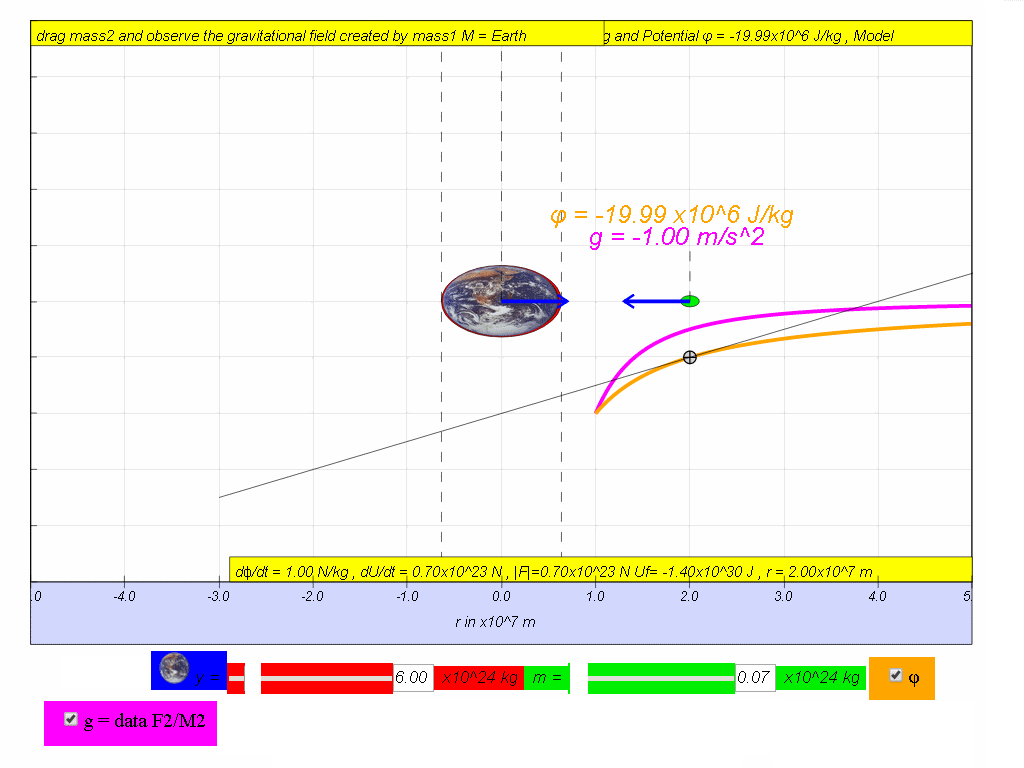
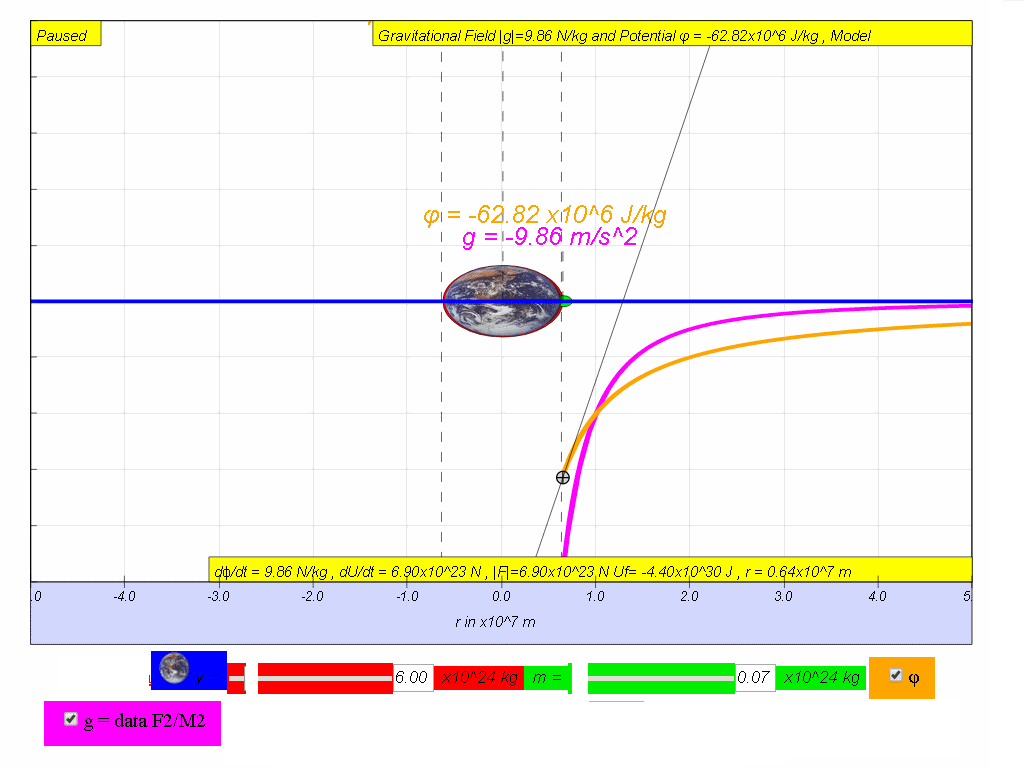
iv) by means of using the simulation, move the mass and record
down and fill in the last 2 missing columns for Gravitational
Field Strength and rate of change of potential with
distance.
v) Hence, suggest a relationship between g and
vi) Explain why the accuracy of determining g at r = 3x107 is poor when using the following values at r = 2x107 and 4x107 m where