Simple
Harmonic Motion
Learning
Outcomes (LOs)
- describe simple examples
of free oscillations.
- investigate the motion
of an oscillator using experimental and graphical methods.
- understand and use the
terms amplitude, period, frequency and angular frequency.
- recognise and use the
equation a = - ω2 x as the defining
equation of simple harmonic motion.
- recall and use x= x0 ω sin( ωt )as a
solution to the equation a = - ω2 x
- recognise and use v = v0 cos ( ω t )
,
- describe with graphical
illustrations, the changes in displacement, velocity and
acceleration during simple harmonic motion.
- describe the interchange
between kinetic and potential energy during simple harmonic
motion.
- describe practical
examples of damped oscillations with particular reference to the
effects of the degree of damping and the importance of critical
damping in cases such as a car suspension system.
- describe practical
examples of forced oscillations and resonance.
- show an appreciation
that there are some circumstances in which resonance is useful
and other circumstances in which resonance should be avoided.
- describe graphically how
the amplitude of a forced oscillation changes with frequency
near to the natural frequency of the system, and understand
qualitatively the factors which determine the frequency response
and sharpness of the resonance.
YouTube
of many examples of oscillators
http://youtu.be/VKtEzKcg6_s This video can be
used at the start of the first lecture (while students settle down
for lecture) to introduce oscillations, to show various modes of
oscillations and to interest them.
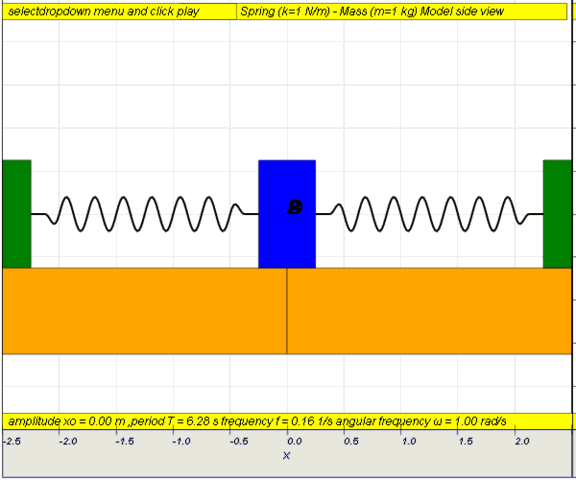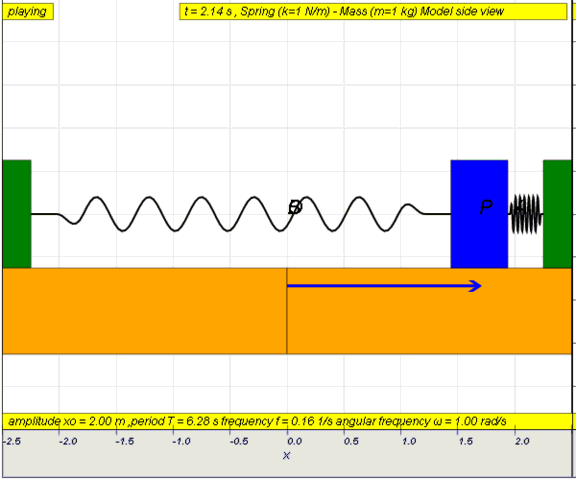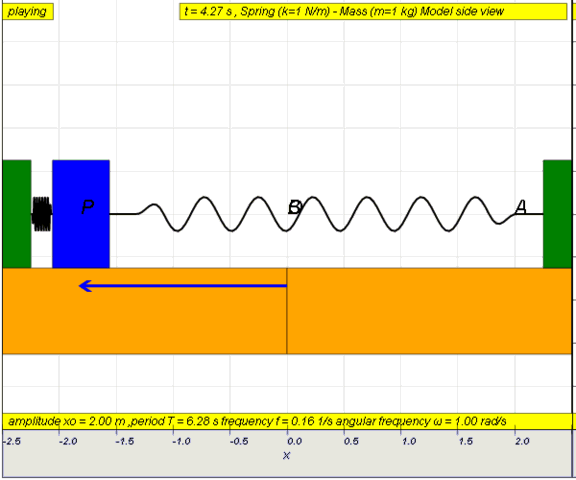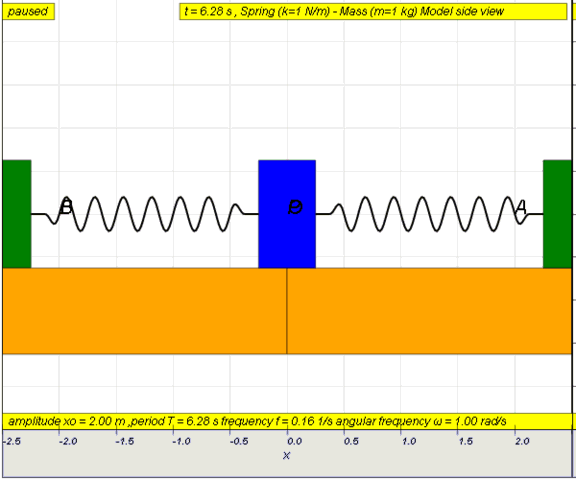
Simple
examples of free oscillations LO(a)
Example
1: Simple pendulum
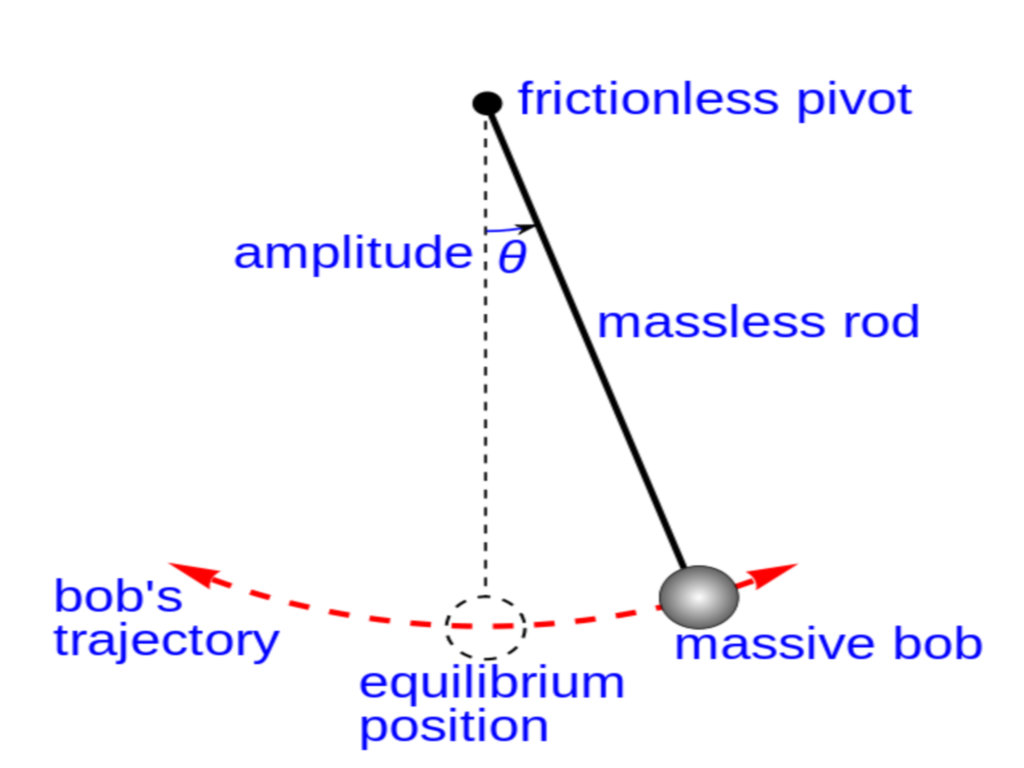
static picture of a pendulum bob given
an initial horizontal displacement and released to swing freely to
produce to and fro motion
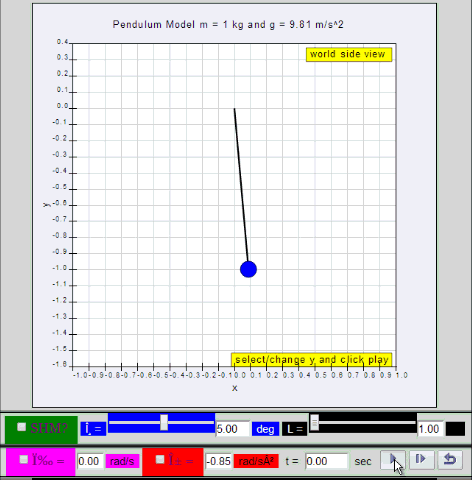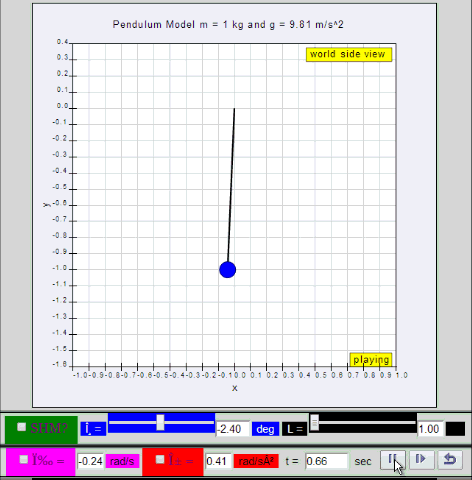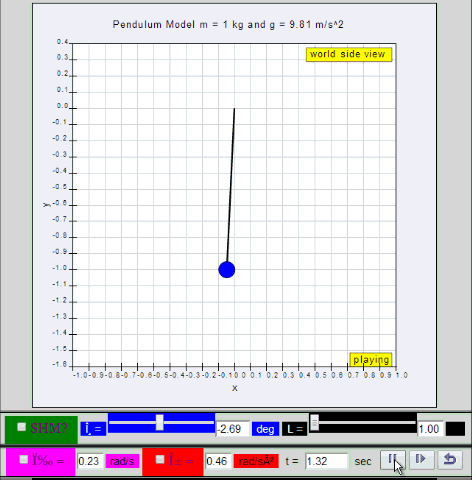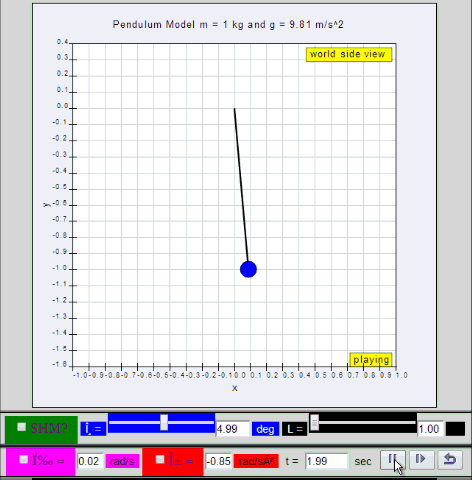
dynamic picture of a pendulum bob given
an initial horizontal displacement and released to swing freely to
produce to and fro motion
http://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHM01/SHM01_Simulation.xhtml
Q1: what is the maximum angle of release
before the motion is not accurately described as a simple harmonic
motion for the case of a simple free pendulum?
A1: : 10 degrees for error of ,
depending on what is the error acceptable, small angle is
typically about less than 10 degree of swing from the vertical.


