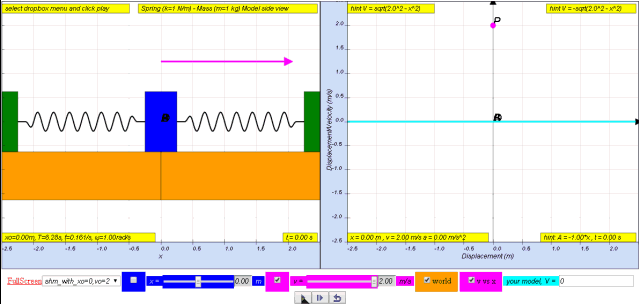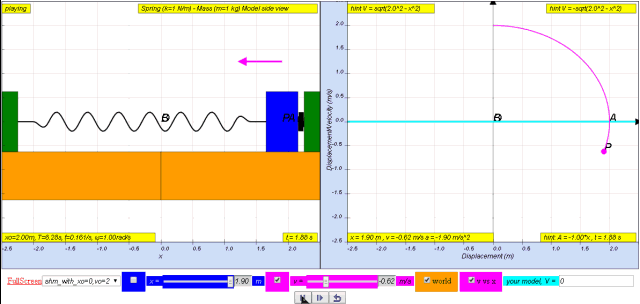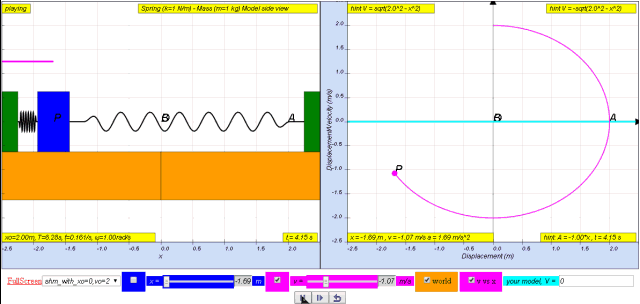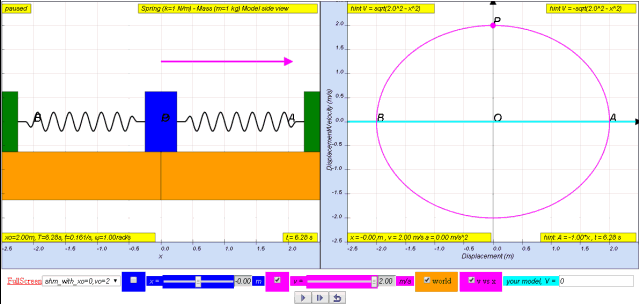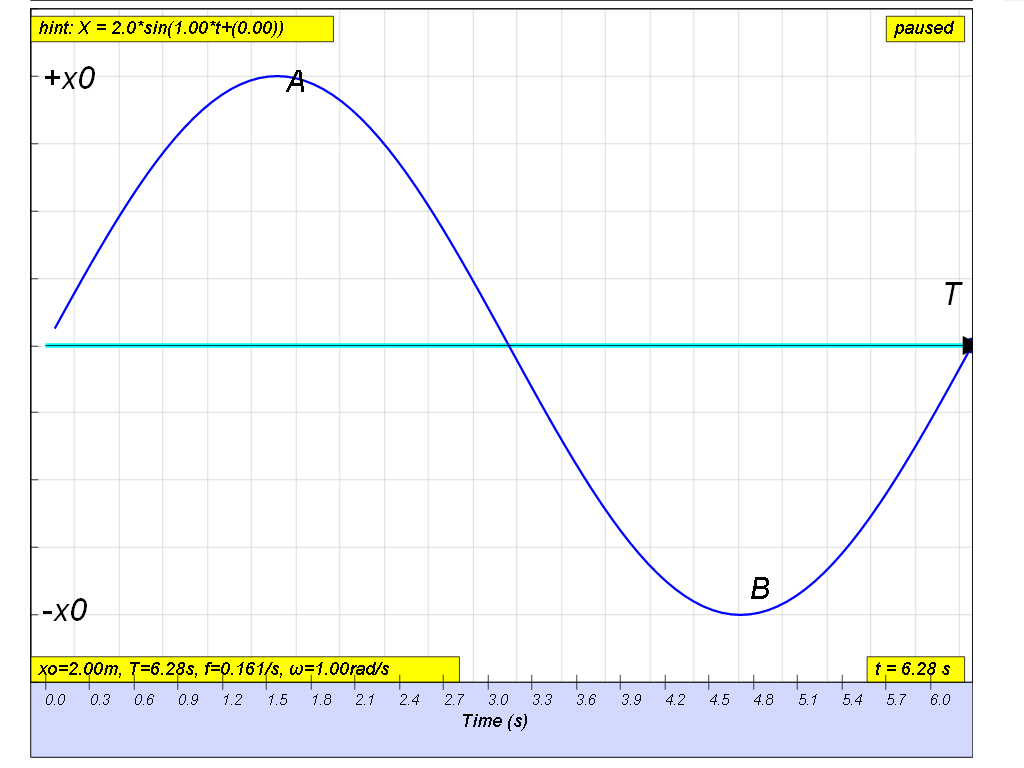
Variation with time of velocity
From x = xo sin ω t
differentiating we get
where
v0 = x0 ω
is the maximum velocity

Variation with time of velocity
From mathematical identity cos2 ωt + sin2 ωt = 1,
rearranging
cos2 ωt = 1 - sin2 ωt
since
v = x0ω cos ωt
where x0 is the maximum displacement
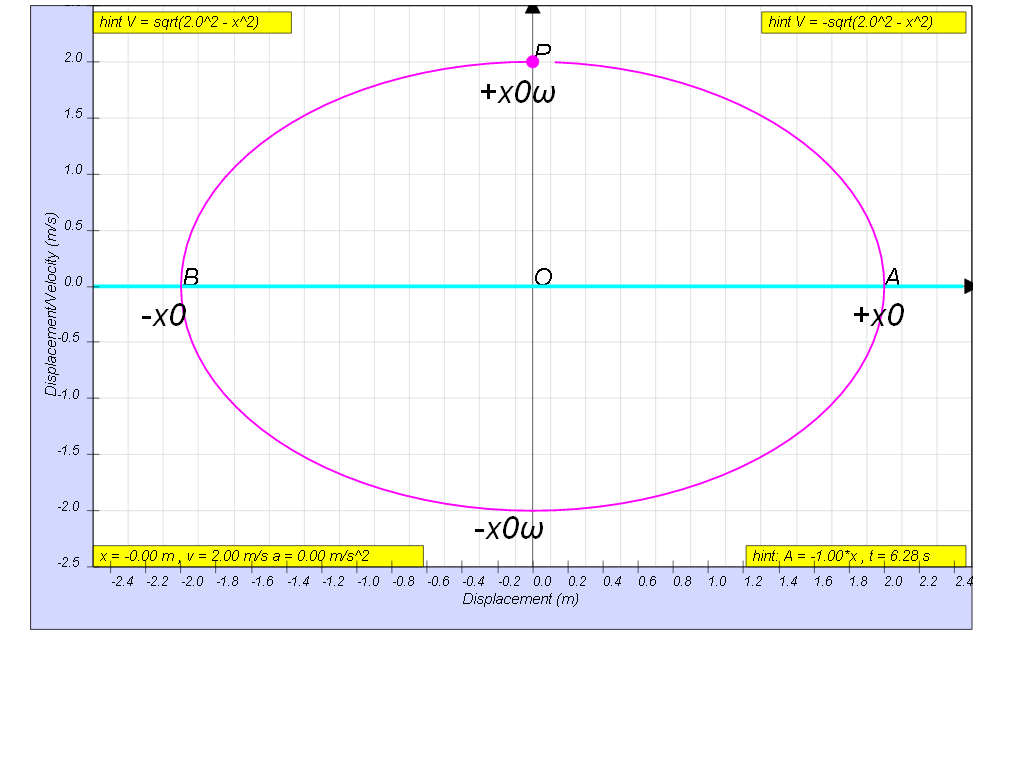
Variation with displacement of velocity