(b)    Variation with Displacement of Energy in Simple Harmonic Motion


Consider a spring of spring constant k connected to a mass m as shown. When the mass is displaced from its equilibrium position by some speed, it will oscillate to the right and left. 
 


At the beginning x=0, t = 0, the energy of the system will consist totally of the mass spring’s kinetic energy (KE). 
From 0 < t < T/4, as the mass moves away from x = 0, the spring pulls the mass towards equilibrium position, this KE is converting to PE as stored spring potential energy.
At the maximum amplitude, x = x0, t = T/4, the all the energy of the system will consist totally of the spring’s potential energy (PE).
From T/4 < t < T/2 as the mass moves towards x = 0, the spring pulls the mass toward the equilibrium position, the potential energy is transformed back into kinetic energy (KE) until at the equilibrium position the kinetic energy will reach a maximum. 
similarly, from T/2 < t < 3T/4, the similar energy conversion occurs but now for negative values of x moving away from equilibrium position .
similarly, from  3T/4 < t < T, the similar energy conversion occurs but now for negative values of x moving towards equilibrium position .

The constant exchange between potential energy PE and kinetic energy KE is essential in maintaining oscillations. The total energy TE, which is the summation of kinetic and potential energy, will always add up to a constant value as shown.





this is how the x vs x looks together of the energy vs x graphs



recalling Energy formula

KE = ½ m v2 
PE =  ½ k x2 therefore, total mechanical energy TE is both KE and PE, can be written as

TE = KE + PE = ½ m v2 + ½ k x2
since  v = ± ( x 0 2 - x 2 ) 

KE = ½ m v2 = ½ m ω2( xo2- x2)

from the simple harmonic motion, we also can get ω = k m 

PE =  ½ k x2 = ½ m ω2x2

therefore, 

TE = KE + PE = ½ m ω2( xo2- x2) + ½ m ω2x2 = ½ m ω2x02

hence or otherwise the table below shows the various formula and their values 

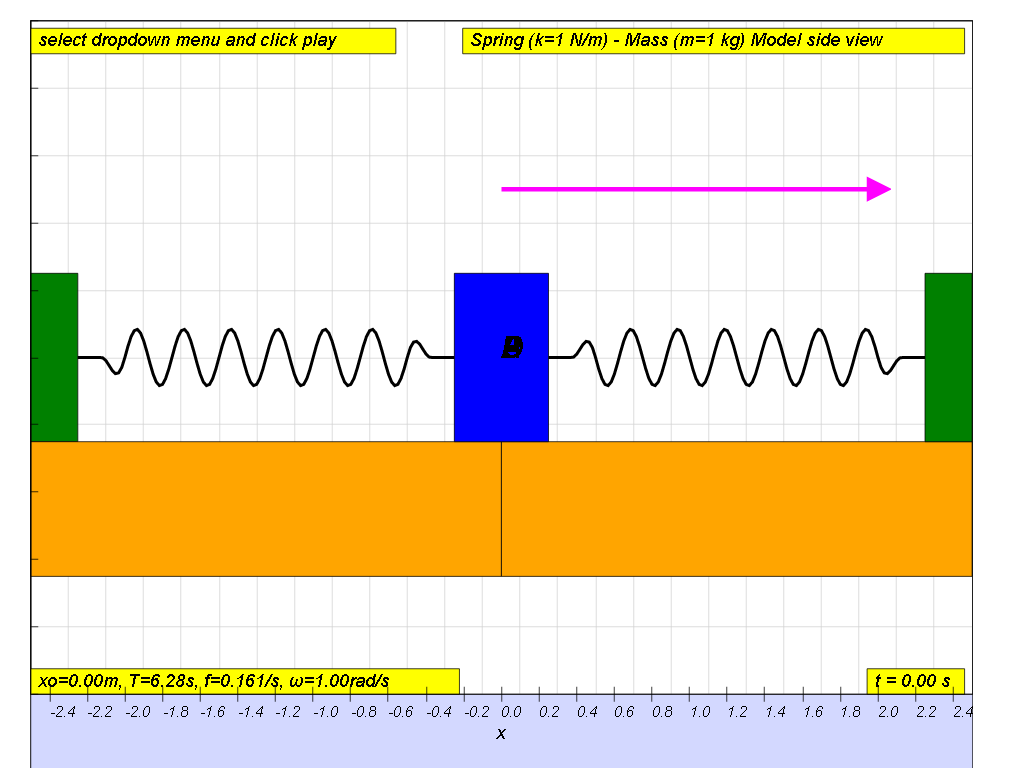
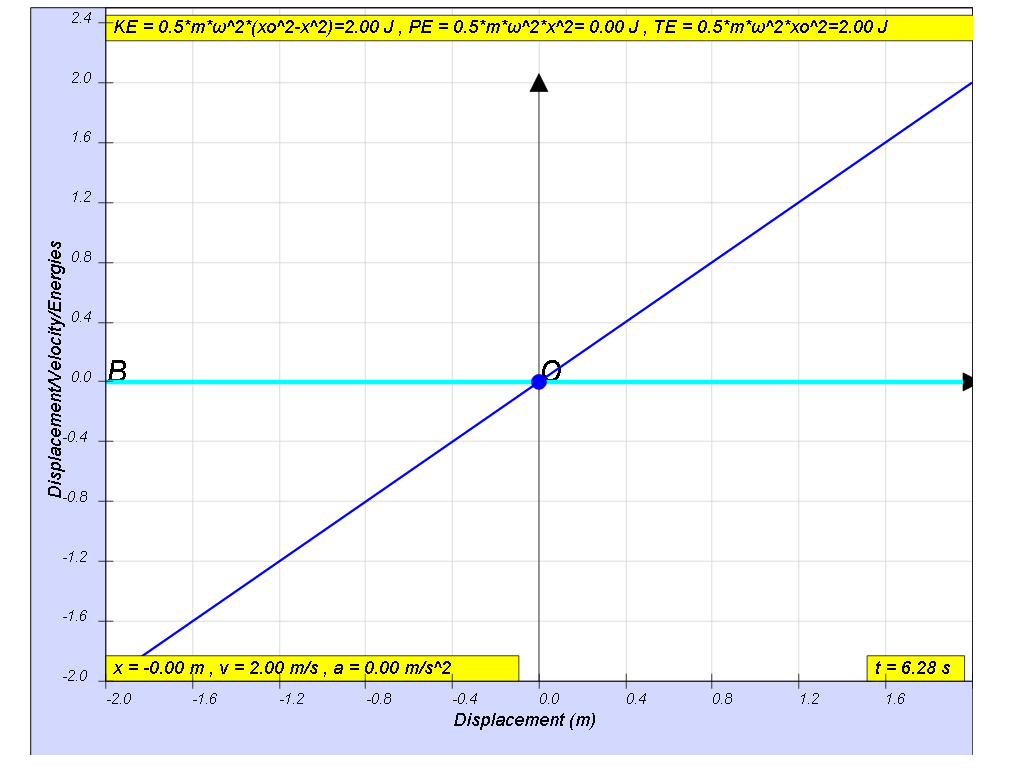
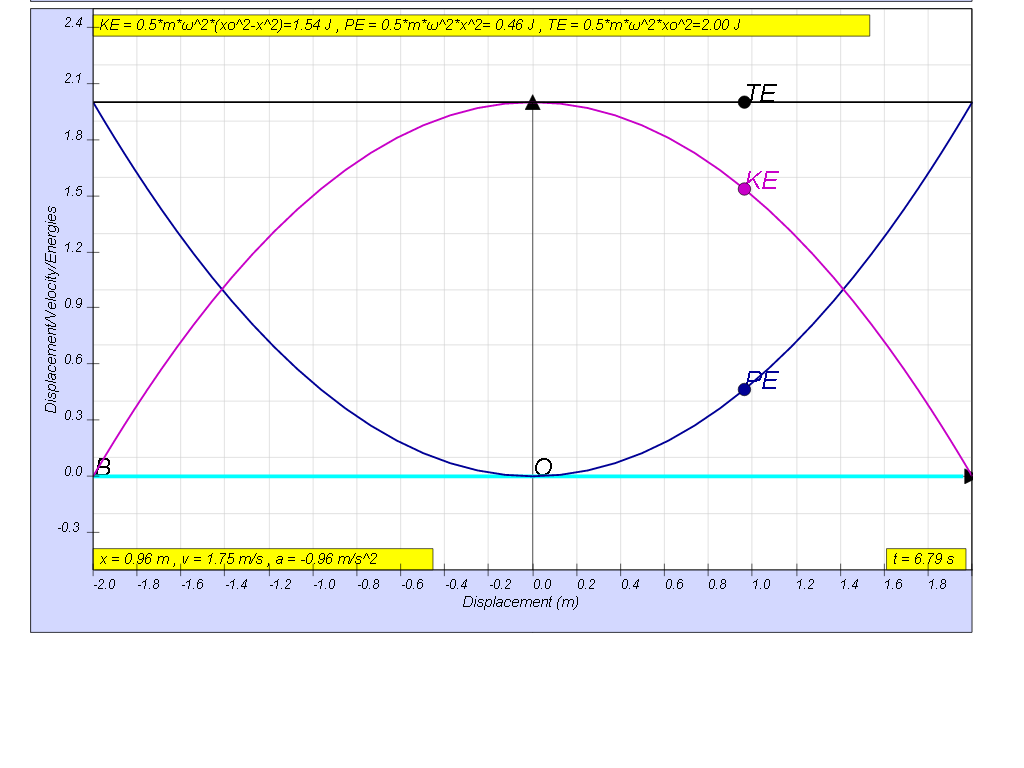
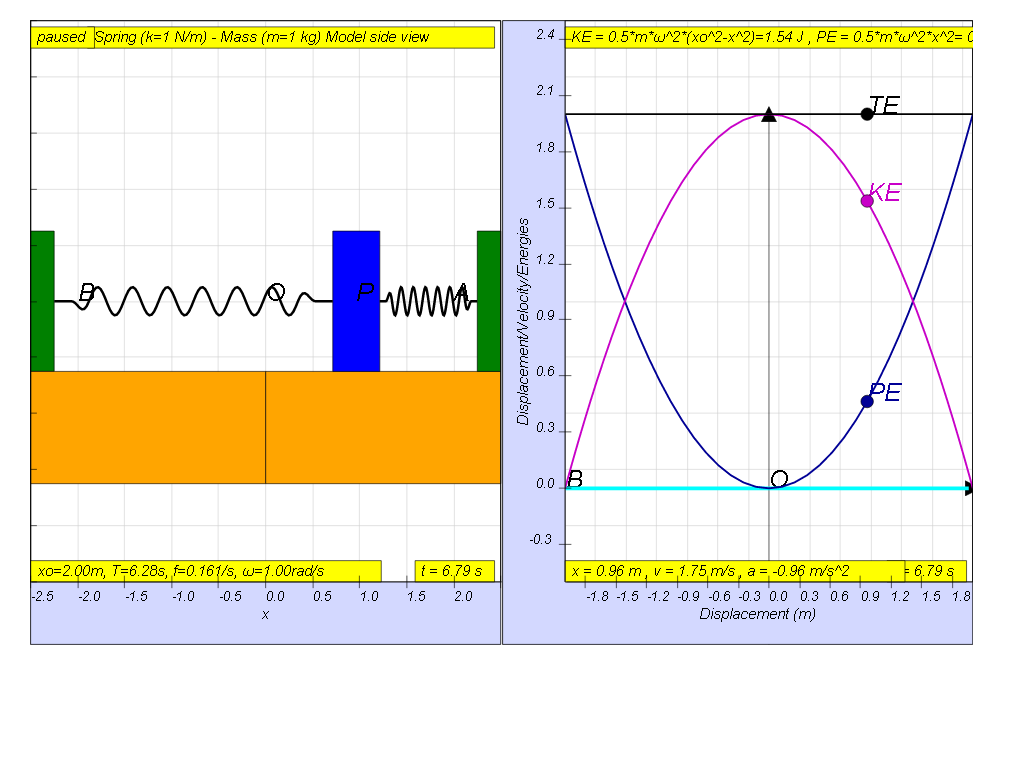
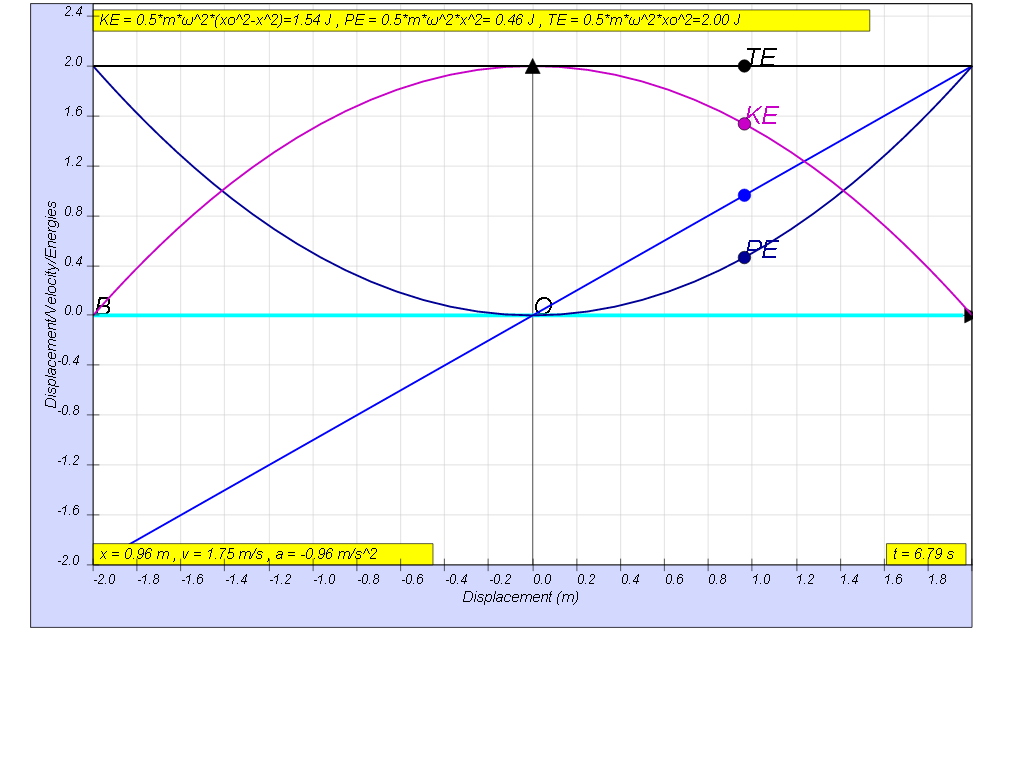
general energy formula SHM energy formula when x = -x0 when x = 0 when x = x0
KE = ½ m v2 KE = ½ m ω2( xo2- x2) 0 ½ m ω2x02 0
PE =  ½ k x2 PE = ½ m ω2x2 ½ m ω2x02 0 ½ m ω2x02
TE = KE + PE
 TE = ½ m ω2( xo2- x2) + ½ m ω2x2 ½ m ω2x02 ½ m ω2x02 ½ m ω2x02


If no energy is lost during an oscillation, then total energy remains constant.

Model:

http://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHM18/SHM18_Simulation.xhtml