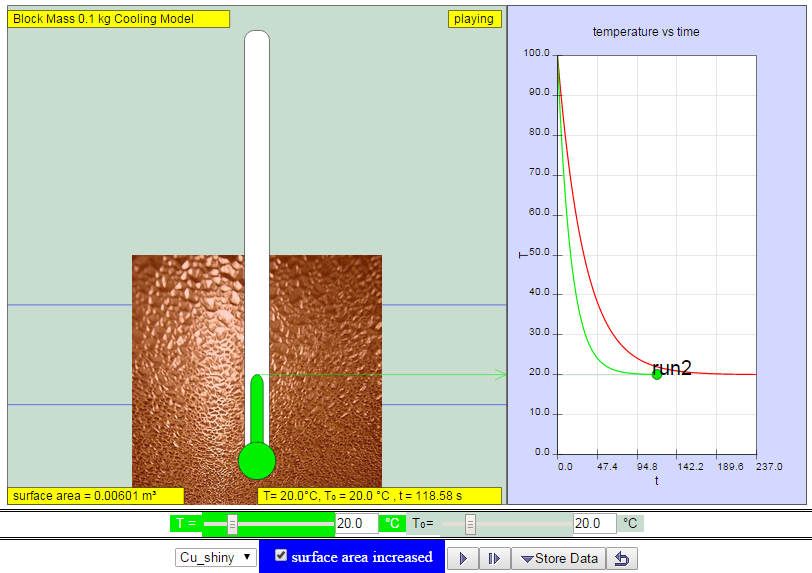
 |
| http://weelookang.blogspot.sg/2014/11/ejss-cube-block-cooling-model.html increasing surface area of copper cube increases rate of heat loss to surrounding model:https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_cooling/cooling_Simulation.xhtml zip model: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_cooling.zip source: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_cooling.zip author: lookang, Christian wolfgang |
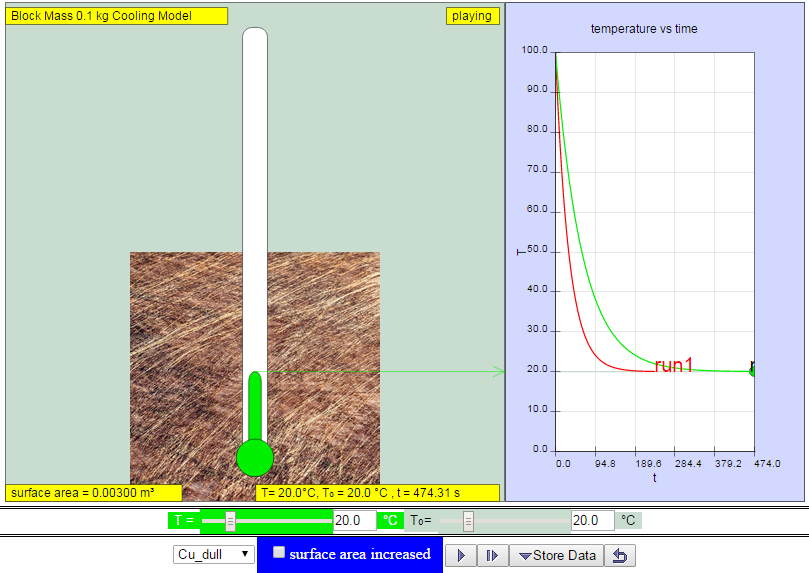 |
| http://weelookang.blogspot.sg/2014/11/ejss-cube-block-cooling-model.html dull copper lose heat slower than shiny copper model:https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_cooling/cooling_Simulation.xhtml zip model: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_cooling.zip source: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_cooling.zip author: lookang, Christian wolfgang |
Newton's Law of Cooling
The Newton's Law of Cooling model computes the temperature of an object of mass M as it is heated or cooled by the surrounding medium.
Assumption:
The model assumes that the temperature T within the object is
uniform.
Validity:
This lumped system approximation is valid if the rate of
thermal energy transfer within the object is faster than the
rate of thermal energy transfer at the surface.
Convection-cooling "Newton's law of cooling" Model:
Newton assumed that the rate of thermal
energy transfer at the object's surface is proportional
to the surface area and to the temperature difference between
the object and the surrounding medium.
δQδt=hA(T(t)−Tbackground)
Definition Specific Heat Capacity:
The specific heat capacity of a material on a per mass basis is
combing the 2 equations
assuming mc is constant'
assuming Tbackground
is a infinite reservoir
therefore
negative sign can be taken out of the differential equation.
let κ=hAmc
If heating is added on,
the final ODE equation looks like
Definition Equation Used:
assumption of increased surface are
Materials added:
copper shinyheat transfer coefficient
copper dull
heat transfer coefficient
aluminium shiny
heat transfer coefficient
aluminium dull
heat transfer coefficient
iron shiny
heat transfer coefficient
iron dull
heat transfer coefficient
Users can select the mass of the object and the material and the model computes the surface area assuming a cubic shape. The model plots the object's temperature as a function of time as the user heats and cools the object. A data-tool button on the temperature graph allows users fit the data to analytic functions.
Note: A typical (rough) heat transfer coefficient h for still air and iron is 6 W/(K m^2) and 400 W/(K m^2) . The Newton's Law of Cooling model assumes h=400 for all shiny and h=200 for dull materials. The actual value of h depends on many parameters including the material, the fluid velocity, the fluid viscosity and the condition of the object's surface.
References:
- "Measuring the Specific Heat of Metals by Cooling," William Dittrich, The Physics Teacher, (in press).
Credits:
- The Newton's Law of Cooling model was created by Wolfgang Christian using the Easy Java Simulations (EJS) version 4.2 authoring and modeling tool.
- EJSS Cube Block Cooling Model was created by Wolfgang Christian and recreated by lookang using the Easy Java Simulations (EJS) version 5.1 authoring and modeling tool