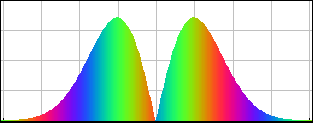
[Screen shot of an SHO superposition state that retains its shape.]

Pre-set Demonstrations

You can access the pre-set initial states for the infinite square well (ISW) and harmonic oscillator (SHO) via the textbox on the lower-left-hand side of the main simulation panel. These show:

ISW Two State: Loads an ISW two-state superposition (equal mix of ground state and first-excited state).

ISW Gaussian: Loads an ISW initial Gaussian wave packet with no initial average momentum.

ISW Narrow Gaussian <p>₀ = 0: Loads an ISW initial Gaussian wave packet with no initial average momentum.

ISW Narrow Gaussian <p>₀ = 80 π/a: Loads an ISW initial Gaussian wave packet with an initial average momentum.

SHO Two State: Loads: Loads a SHO two-state superposition (equal mix of ground state and first-excited state).

SHO Squeezed: Loads: Loads a SHO coherent state with an initial average momentum.

SHO Squeezed Wide: Loads a SHO coherent state with an initial average momentum.

SHO Boosted Coherent: Loads a SHO coherent state with an initial average momentum.

SHO Boosted Squeezed: Loads a SHO squeezed state with an initial average momentum.

SHO Shifted Ground State: Loads the SHO ground state with an initial shift from x = 0.

SHO Shifted Excited State: Loads the SHO first-excited state with an initial shift from x = 0.

Superposition Principle

The fundamental building blocks of one-dimensional quantum mechanics are energy eigenfunctions ψ_n(x) and energy eigenvalues E_n. For a given potential energy function V(x) and boundary conditions, energy eigenfunctions can be determined either analytically or numerically. Most of the time in quantum mechanics these energy eigenfunctions are determined in position space. Once these energy eigenstates are determined, more interesting quantum-mechanical wave functions Ψ(x,t) can be studied by applying the superposition principle

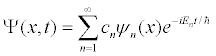
superposition principle equation

where the expansion coefficients c_n satisfy Σ |c_n|² = 1. Depending on how many of the coefficients c_n are non-zero, one may have an energy eigenstate, a two-state superposition, or even an initially localized (usually Gaussian shaped) wave packet.

Any complete orthonormal set of eigenfunctions can be used to construct the wave function Ψ(x,t). This simulation uses the superposition principle to construct and display a time-dependent wave function using either infinite square well (ISW) or simple harmonic oscillator (SHO) eigenfunctions.

Units

Although the metric (MKS) system of units has become the standard international system of units, it is not well suited for computation if the quantities being computed are very large or very small. Quantum phenomena occurs on the microscopic scale at very fast times and computations are usually done using an atomic system of units in which the reduced Plank's constant ħ, the Bohr radius a_o, and the mass of the electron m are set equal to unity. The one-dimensional time independent Schrödinger equation in these units is:

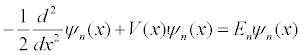
In atomic units, one unit time is 2.42×10^-17 seconds, one unit of distance is 5.29×10^-11 meters, and one unit of energy is 4.36×10^-18 Joules. This simulation models a particle with the mass of an electron using these atomic units.

References:

E. H. Kennard, "The quantum mechanics of an electron or other particle," J. Franklin Institute 207 47-78 (1929); see also "Zur Quantenmechanik einfacher Bewegungstypen" (translated as "The quantum mechanics of simple types of motion"), Z. Phys. 44 326-352 (1927).
C. Dean, "Simple Schrodinger wave functions which simulate classical radiating systems," Am. J. Phys. 27, 161-163 (1959).
For a review of revival phenomena, see R. W. Robinett, "Quantum wave packet revivals," Phys. Rep. 392, 1-119 (2004).
R. W. Robinett, M. A. Doncheski, and L. C. Bassett, "Simple forms of position-momentum correlated Gaussian free-particle wave packets in one dimension with the general form of the time-dependent spread in position," Found. Phys. Lett. 18 455-475 (2005).
D. F. Styer, "Quantum revivals versus classical periodicity in the infinite square well," Am. J. Phys. 69 56-62 (2001).
M. Andrews, "Wave packets bouncing off walls," Am. J. Phys. 66 252-254 (1998).
V. V. Dodonov and M. A. Andreata, "Shrinking quantum packets in one dimension," Phys. Lett. A 310 101-109 (2003).
I. Sh. Averbukh and N. F. Perelman, "Fractional revivals: Universality in the long-term evolution of quantum wave packets beyond the correspondence principle dynamics," Phys. Lett. A139 449-453 (1989); "Fractional revivals of wave packets," Acta Phys. Pol. 78 33-40 (1990).
M. Belloni, M. A. Doncheski, and R. W. Robinett, "Wigner quasi-probability distribution for the infinite square well: Energy eigenstates and time-dependent wave packets," Am. J. Phys. 72 1183-1192 (2004).

Credits:

The Eigenstate Superposition Demonstration simulation was created by Wolfgang Christian and the narrative was written by Wolfgang Christian and Mario Belloni.

Note:

The eigenstate superposition simulation was created using the Easy Java Simulations (EJS) modeling tool. You can examine and modify the model for this simulation if you have EJS installed by right-clicking within the wave function plot and selecting "Open Ejs Model" from the pop-up menu. Information about Ejs is available at: <http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection <http://www.compadre.org/OSP/>.